R and Shiny Training: If you find this blog to be interesting, please note that I offer personalized and group-based training sessions that may be reserved through Buy me a Coffee. Additionally, I provide training services in the Spanish language and am available to discuss means by which I may contribute to your Shiny project.
Motivation
I got more than 3 questions about the use of Student’s t-test in the last week. I think it is a good idea to write a blog post about it.
What is Student’s t-test?
Student’s t-test is a statistical test that is used to compare the mean of a group against a specified value and to compare the means of two groups against each other. For example, to evaluate if the mean speed of electric and water Pokemon are statistically different. Student wasn’t the name of the test’s creator. The name of the creator was William Gosset, but he published his work under the pseudonym “Student”, like Madonna or Prince.
When we use the test we aim at finding differences that are statistically different. What do we mean by that? Let’s consider the next averages for the different Pokemon type:
if (!require(dplyr)) install.packages("dplyr")
library(dplyr)
# download from https://github.com/pachadotdev/blog-materials/raw/refs/heads/main/2023/06/24/pokemon.rds
pokemon <- readRDS("~/Documents/blog-materials/2023/06/24/pokemon.rds")
pokemon %>%
select(type_1, attack, defense, speed) %>%
group_by(type_1) %>%
summarise_if(is.numeric, mean, na.rm = TRUE) %>%
arrange(type_1) %>%
print(n = 15)
# A tibble: 15 × 4
type_1 attack defense speed
<fct> <dbl> <dbl> <dbl>
1 Bug 63.8 57.1 57.1
2 Dragon 94 68.3 66.7
3 Electric 62 64.7 98.9
4 Fairy 57.5 60.5 47.5
5 Fighting 103. 61 66.1
6 Fire 83.9 62.6 84
7 Ghost 50 45 95
8 Grass 70.7 69.6 52.1
9 Ground 81.9 86.2 58.1
10 Ice 67.5 67.5 90
11 Normal 67.7 53.5 69.3
12 Poison 74.4 67 58.8
13 Psychic 60.1 57.5 93
14 Rock 82.2 110 58.3
15 Water 70.2 77.5 67.7
In the table, the means speed for electric and water pokemon are 98.9 and 67.7 pokemon measurement points (pmp), and we know that those two numbers are different. The question becomes: *Is the difference between 98.9 and 67.7 pmp statistically different from zero? Or in other words, is the difference due to chance or is it due to a real difference between the groups?
We define a null hypothesis, such as “the means for electric an water pokemon are equal” and an alternative hypothesis, such as “the means for electric and water pokemon are different”. The observations support evidence to reject or fail to reject the null hypothesis. In Statistics we never accept the null hypothesis, we just fail to reject it. To read more about inference and hypothesis testing, I recommend Introduction to Modern Statistics by Mine Çetinkaya-Rundel and Johanna Hardin.
Comparing the means of two groups
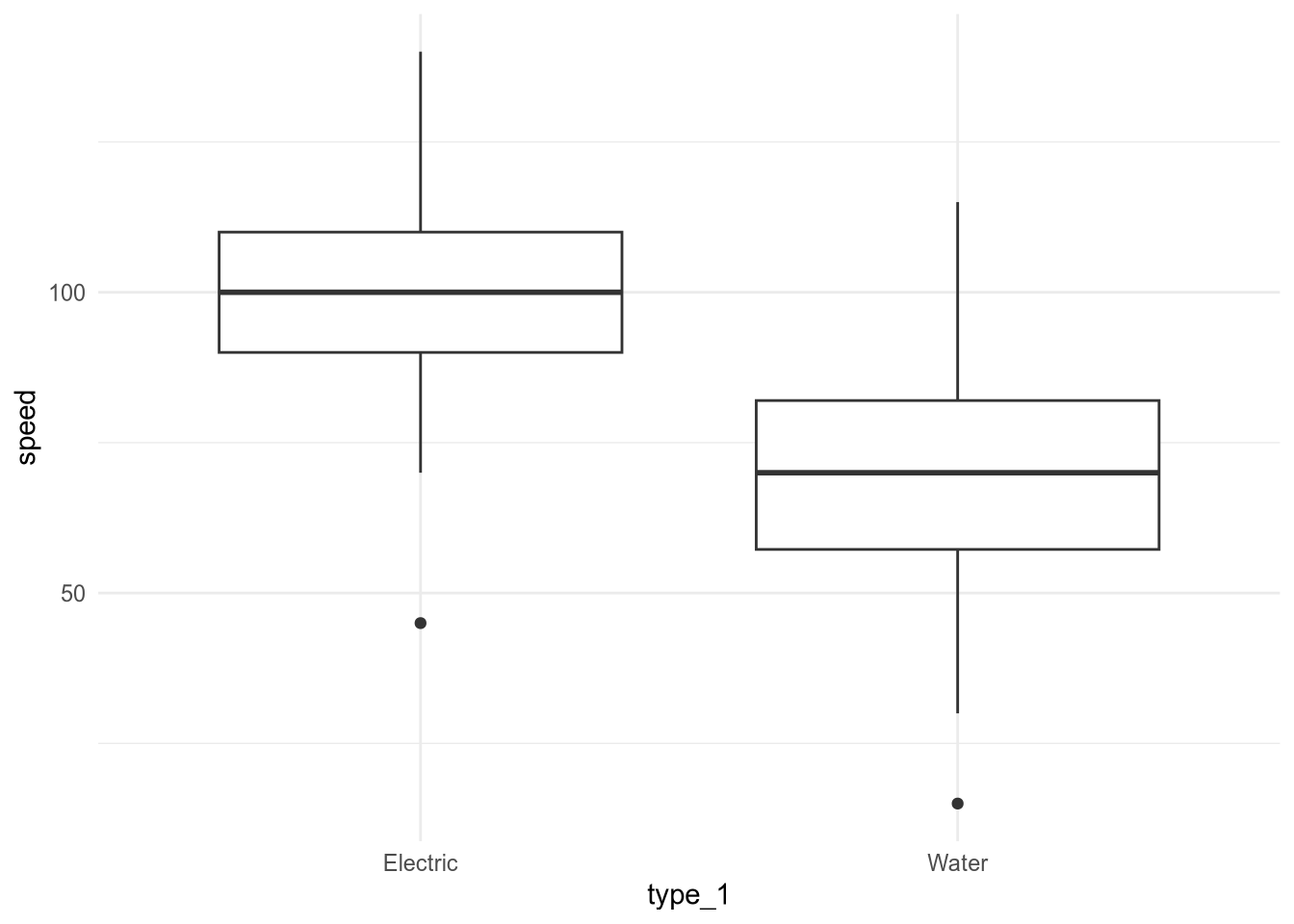
From the previous example, we can define \(H_0: \mu^{\text{electric}} = \mu^{\text{water}}\) and \(H_1: \mu^{\text{electric}} \neq \mu^{\text{water}}\). Before proceeding to the formal test, let’s explore the quantiles and the box and whiskers for both groups.
pokemon %>%
filter(type_1 == "Electric") %>%
pull(speed) %>%
quantile(na.rm = TRUE)
0% 25% 50% 75% 100%
45 90 100 110 140
pokemon %>%
filter(type_1 == "Water") %>%
pull(speed) %>%
quantile(na.rm = TRUE)
0% 25% 50% 75% 100%
15.00 57.25 70.00 82.00 115.00
if (!require(ggplot2)) install.packages("ggplot2")
library(ggplot2)
pokemon %>%
filter(type_1 %in% c("Electric", "Water")) %>%
ggplot() +
geom_boxplot(aes(x = type_1, y = speed)) +
theme_minimal()
From the quantiles and the plot we already have an intution. If we move one box on top of the other, the central quantiles do not overlap, suggesting that there is a statistically significant difference.
The the t.test function in R by default returns the p-value of a two sided test.
electric <- pokemon %>%
filter(type_1 == "Electric") %>%
pull(speed) %>%
na.omit()
water <- pokemon %>%
filter(type_1 == "Water") %>%
pull(speed) %>%
na.omit()
t.test(electric, water)
Welch Two Sample t-test
data: electric and water
t = 2.9897, df = 11.019, p-value = 0.01228
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
8.22914 54.12007
sample estimates:
mean of x mean of y
98.88889 67.71429
The calculated p-value is 0.01228 which is less than the critical p-value 0.05. We reject the null hypothesis that the means of the two groups are equal. We conclude that the means of the two groups are different.
What if we are interested in the sign of the alternative hypothesis? We can use the alternative argument in the t.test function. For example, if we want to specify the alternative \(H_1: \mu^{\text{electric}} > \mu^{\text{water}}\) for the same \(H_0\), we specify the alternative = "greater" argument.
t.test(electric, water, alternative = "greater")
Welch Two Sample t-test
data: electric and water
t = 2.9897, df = 11.019, p-value = 0.006141
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
12.45138 Inf
sample estimates:
mean of x mean of y
98.88889 67.71429
The calculated p-value is 0.00614 which is less than the critical p-value 0.05. We reject the null hypothesis that the means of the two groups are equal. We conclude that the mean of the electric group is statistically greater than the mean of the water group.
As another example, if we want to specify the alternative \(H_1: \mu^{\text{electric}} < \mu^{\text{water}}\) for the same \(H_0\), we specify the alternative = "less" argument.
t.test(electric, water, alternative = "less")
Welch Two Sample t-test
data: electric and water
t = 2.9897, df = 11.019, p-value = 0.9939
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf 49.89783
sample estimates:
mean of x mean of y
98.88889 67.71429
The calculated p-value is 0.9939 which is greater than the critical p-value 0.05. We fail to reject the null hypothesis that the means of the two groups are equal. We conclude that the mean of the electric group is statistically equal than the mean of the water group.
Exercises
Repeat the previous analysis for the attack and defense variables for two Pokemon types of your choice.
Repeat the previous analysis for a critical p-value 0.01 and 0.1.
Find a clinical dataset and perform a Student’s t-test for the trial and control groups. Would you be interested in a particular type of alternative hypothesis? Why?
Notes
The usual p-value is 0.05 is just a convention to work with confidence level of 95% (100% - 5%).
The direction of the inequality in the alternative hypothesis depends on the order of the groups in the t.test function.